Archive for the 'accounting identities' Category

Keynes and Accounting Identities

Published October 20, 2015 accounting identities , Hawtrey , Irving Fisher , Keynes , Michael Pettis , savings-investment identity , Uncategorized 39 Comments
Tags: , ,

In a post earlier this week, Michael Pettis was kind enough to refer to a passage from Ralph Hawtrey’s review of Keynes’s General Theory, which I had quoted in an earlier post, criticizing Keynes’s reliance on accounting identities to refute the neoclassical proposition that it is the rate of interest which equilibrates savings and investment. Here’s what Pettis wrote:

Keynes, who besides being one of the most intelligent people of the 20th century was also so ferociously logical (and these two qualities do not necessarily overlap) that he was almost certainly incapable of making a logical mistake or of forgetting accounting identities. Not everyone appreciated his logic. For example his also-brilliant contemporary (but perhaps less than absolutely logical), Ralph Hawtrey, was “sharply critical of Keynes’s tendency to argue from definitions rather than from causal relationships”, according to FTC economist David Glasner, whose gem of a blog, Uneasy Money, is dedicated to reviving interest in the work of Ralph Hawtrey. In a recent entry Glasner quotes Hawtrey:

[A]n essential step in [Keynes’s] train of reasoning is the proposition that investment and saving are necessarily equal. That proposition Mr. Keynes never really establishes; he evades the necessity doing so by defining investment and saving as different names for the same thing. He so defines income to be the same thing as output, and therefore, if investment is the excess of output over consumption, and saving is the excess of income over consumption, the two are identical. Identity so established cannot prove anything. The idea that a tendency for investment and saving to become different has to be counteracted by an expansion or contraction of the total of incomes is an absurdity; such a tendency cannot strain the economic system, it can only strain Mr. Keynes’s vocabulary.

This is a very typical criticism of certain kinds of logical thinking in economics, and of course it misses the point because Keynes is not arguing from definition. It is certainly true that “identity so established cannot prove anything”, if by that we mean creating or supporting a hypothesis, but Keynes does not use identities to prove any creation. He uses them for at least two reasons. First, because accounting identities cannot be violated, any model or hypothesis whose logical corollaries or conclusions implicitly violate an accounting identity is automatically wrong, and the model can be safely ignored. Second, and much more usefully, even when accounting identities have not been explicitly violated, by identifying the relevant identities we can make explicit the sometimes very fuzzy assumptions that are implicit to the model an analyst is using, and focus the discussion, appropriately, on these assumptions.

I agree with Pettis that Keynes had an extraordinary mind, but even great minds are capable of making mistakes, and I don’t think Keynes was an exception. And on the specific topic of Keynes’s use of the accounting identity that expenditure must equal income and savings must equal investment, I think that the context of Keynes’s discussion of that identity makes it clear that Keynes was not simply invoking the identity to prevent some logical slipup, as Pettis suggests, but was using it to deny the neoclassical Fisherian theory of interest which says that the rate of interest represents the intertemporal rate of substitution between present and future goods in consumption and the rate of transformation between present and future goods in production. Or, in less rigorous terminology, the rate of interest reflects the marginal rate of time preference and the marginal rate of productivity of capital. In its place, Keynes wanted to substitute a pure monetary or liquidity-preference theory of the rate of interest.

Keynes tried to show that the neoclassical theory could not possibly be right, inasmuch as, according to the theory, the equilibrium rate of interest is the rate that equilibrates the supply of with the demand for loanable funds. Keynes argued that because investment and savings are identically equal, savings and investment could not determine the rate of interest. But Keynes then turned right around and said that actually the equality of savings and investment determines the level of income. Well, if savings and investment are identically equal, so that the rate of interest can’t be determined by equilibrating the market for loanable funds, it is equally impossible for savings and investment to determine the level of income.

Keynes was unable to distinguish the necessary accounting identity of savings and investment from the contingent equality of savings and investment as an equilibrium condition. For savings and investment to determine the level of income, there must be some alternative definition of savings and investment that allows them to be unequal except at equilibrium. But if there are alternative definitions of savings and investment that allow those magnitudes to be unequal out of equilibrium — and there must be such alternative definitions if the equality of savings and investment determines the level of income — there is no reason why the equality of savings and investment could not be an equilibrium condition for the rate of interest. So Keynes’s attempt to refute the neoclassical theory of interest failed. That was Hawtrey’s criticism of Keynes’s use of the savings-investment accounting identity.

Pettis goes on to cite Keynes’s criticism of the Versailles Treaty in The Economic Consequences of the Peace as another example of Keynes’s adroit use of accounting identities to expose fallacious thinking.

A case in point is The Economic Consequences of the Peace, the heart of whose argument rests on one of those accounting identities that are both obvious and easily ignored. When Keynes wrote the book, several members of the Entente – dominated by England, France, and the United States – were determined to force Germany to make reparations payments that were extraordinarily high relative to the economy’s productive capacity. They also demanded, especially France, conditions that would protect them from Germany’s export prowess (including the expropriation of coal mines, trains, rails, and capital equipment) while they rebuilt their shattered manufacturing capacity and infrastructure.

The argument Keynes made in objecting to these policies demands was based on a very simple accounting identity, namely that the balance of payments for any country must balance, i.e. it must always add to zero. The various demands made by France, Belgium, England and the other countries that had been ravaged by war were mutually contradictory when expressed in balance of payments terms, and if this wasn’t obvious to the former belligerents, it should be once they were reminded of the identity that required outflows to be perfectly matched by inflows.

In principle, I have no problem with such a use of accounting identities. There’s nothing wrong with pointing out the logical inconsistency between wanting Germany to pay reparations and being unwilling to accept payment in anything but gold. Using an accounting identity in this way is akin to using the law of conservation of energy to point out that perpetual motion is impossible. However, essentially the same argument could be made using an equilibrium condition for the balance of payments instead of an identity. The difference is that the accounting identity tells you nothing about how the system evolves over time. For that you need a behavioral theory that explains how the system adjusts when the equilibrium conditions are not satisfied. Accounting identities and conservation laws don’t give you any information about how the system adjusts when it is out of equilibrium. So as Pettis goes on to elaborate on Keynes’s analysis of the reparations issue, one or more behavioral theories must be tacitly called upon to explain how the international system would adjust to a balance-of-payments disequilibrium.

If Germany had to make substantial reparation payments, Keynes explained, Germany’s capital account would tend towards a massive deficit. The accounting identity made clear that there were only three possible ways that together could resolve the capital account imbalance. First, Germany could draw down against its gold supply, liquidate its foreign assets, and sell domestic assets to foreigners, including art, real estate, and factories. The problem here was that Germany simply did not have anywhere near enough gold or transferable assets left after it had paid for the war, and it was hard to imagine any sustainable way of liquidating real estate. This option was always a non-starter.

Second, Germany could run massive current account surpluses to match the reparations payments. The obvious problem here, of course, was that this was unacceptable to the belligerents, especially France, because it meant that German manufacturing would displace their own, both at home and among their export clients. Finally, Germany could borrow every year an amount equal to its annual capital and current account deficits. For a few years during the heyday of the 1920s bubble, Germany was able to do just this, borrowing more than half of its reparation payments from the US markets, but much of this borrowing occurred because the great hyperinflation of the early 1920s had wiped out the country’s debt burden. But as German debt grew once again after the hyperinflation, so did the reluctance to continue to fund reparations payments. It should have been obvious anyway that American banks would never accept funding the full amount of the reparations bill.

What the Entente wanted, in other words, required an unrealistic resolution of the need to balance inflows and outflows. Keynes resorted to accounting identities not to generate a model of reparations, but rather to show that the existing model implicit in the negotiations was contradictory. The identity should have made it clear that because of assumptions about what Germany could and couldn’t do, the global economy in the 1920s was being built around a set of imbalances whose smooth resolution required a set of circumstances that were either logically inconsistent or unsustainable. For that reason they would necessarily be resolved in a very disruptive way, one that required out of arithmetical necessity a substantial number of sovereign defaults. Of course this is what happened.

Actually, if it had not been for the insane Bank of France and the misguided attempt by the Fed to burst the supposed stock-market bubble, the international system could have continued for a long time, perhaps indefinitely, with US banks lending enough to Germany to prevent default until rapid economic growth in the US and western Europe enabled the Germans to service their debt and persuaded the French to allow the Germans to do so via an export surplus. Instead, the insane Bank of France, with the unwitting cooperation of the clueless (following Benjamin Strong’s untimely demise) Federal Reserve precipitated a worldwide deflation that triggered that debt-deflationary downward spiral that we call the Great Depression.

JKH on the Keynesian Cross and Accounting Identities

Published April 14, 2015 accounting identities , JKH , R. G. Lipsey 15 Comments
Tags:

Since beginning this series of posts about accounting identities and their role in the simple Keynesian model, I have received a lot of comments from various commenters, but none has been more persistent, penetrating, and patient in his criticisms than JKH, and I have to say that he has forced me to think very carefully, more carefully than I had ever done before, about my objections to forcing the basic Keynesian model to conform to the standard national income accounting identities. So, although we have not (yet?) reached common ground about how to understand the simple Keynesian model, I can say that my own understanding of how the model works (or doesn’t) is clearer than it was when the series started, so I am grateful to JKH for engaging me in this discussion, even though it has gone on a lot longer than I expected, or really wanted, it to.

In response to my previous post in the series, JKH offered a lengthy critical response. Finding his response difficult to understand and confusing, I wrote a rejoinder that prompted JKH to write a series of further comments. Being preoccupied with a couple of other posts and life in general, I was unable to respond to JKH until now. Given the delay in my response, I decided to respond to JKH in a separate post. I start with JKH’s explanation of how an increase in investment spending is accounted for.

First, the investment injection creates income that accrues to the factors of production – labor and capital. This works through cost accounting. The price at which the investment good is sold covers all costs – including the cost of capital. That said, the price may not cover the theoretical “hurdle rate” for the cost of capital. But that is a technical detail. The equity holders earn some sort of actual residual return, positive or negative. So in the more general sense, the actual cost of capital is accounted for.

So the investment injection creates an equivalent amount of income.

No one says that investment expenditure will not generate an equivalent amount of income; what is questionable is whether the income accrues to factors of production instantaneously. JKH maintains that cost accounting ensures that the accrual is instantaneous, but the recording of a bookkeeping entry is not the same as the receipt of income by households, whose consumption and savings decisions are the key determinant of income adjustments in the Keynesian model. See the tacit assumption in the sentence immediately following.

Consider the effect at the moment the income is fully accrued to the factors of production – before anything else happens.

I understand this to mean that income accrues to factors of production the instant expenditure is booked by the manufacturer of the investment goods; otherwise, I don’t understand why this occurs “before anything else happens.” In a numerical example, JKH posits an increase in investment spending of 100, which triggers added production of 100. For purposes of this discussion, I stipulate that there is no lag between expenditure and output, but I don’t accept that income must accrue to workers and owners of the firm instantaneously as output occurs. Most workers are paid per unit of time, wages being an hourly rate based on the number of hours credited per pay period, and salaries being a fixed amount per pay period. So there is no immediate and direct relationship between worker input into the production process and the remuneration received. The additional production associated with the added investment expenditure and production may or may not be associated with any additional payments to labor depending on how much slack capacity is available to firms and on how the remuneration of workers employed in producing the investment goods is determined.

That amount of income must be saved by the macroeconomy – other things equal. We know this because no new consumer goods or services are produced in this initial standalone scenario of a new investment injection. Therefore, given that saving in the generic sense is income not used to purchase consumer goods and services, this new income created by an assumed investment injection must be saved in the first instance.

Since it is quite conceivable (especially if there is unused capacity available to the firm) that producing new investment goods will not change the total remuneration received by (or owed to) workers in the current period, all additional revenue collected by the firm accruing entirely to the owners of the firm, revenue that might not be included in the next scheduled dividend payment by the firm to shareholders, I am not persuaded that it is unreasonable to assume that there is a lag between expenditure on goods and services and the accrual of income to factors of production. At any rate, whether the firm’s revenue is instantaneously transmuted into household income does not seem to be a question that can be answered in only one way.

What the macroeconomy “must” do is an interesting question, but in the basic Keynesian model, income is earned by households, and it is households, not an abstraction called the macroeconomy, that decide how much to consume and how much to save out of their income. So, in the Keynesian model, regardless of the accounting identities, the relevant saving activity – the saving activity specified by the marginal propensity to save — is the saving of households. That doesn’t mean that the model cannot be extended or reconstructed to allow for saving to be carried out by business firms or by other entities, but that is not how the model, at its most basic level, is set up.

So at this incipient stage before the multiplier process starts, S equals I. That’s before the marginal propensity to consume or save is in motion.

One’s eyes may roll at this point, since the operation of the MPC includes the complementary MPS, and the MPS is a saving function that also operates as the multiplier iterates with successive waves of income creation and consumption.

I understand these two sentences to be an implicit concession that the basic Keynesian model is not being presented in the way it is normally presented in textbooks, a concession that accords with my view that the basic Keynesian model does not always dovetail with the national income identities. Lipsey and I say: don’t impose the accounting identities on the Keynesian model when they are at odds; JKH says reconfigure the basic Keynesian model so that it is consistent with the accounting identities. Where JKH and I may perhaps agree is that the standard textbook story about the adjustment process following a change in spending parameters, in which unintended inventory accumulation corresponding to the frustration of individual plans plays a central role, does not follow from the basic Keynesian model.

So one may ask – how can these apparently opposing ideas be reconciled – the contention that S equals I at a point when the multiplier saving dynamic hasn’t even started?

The investment injection results in an equivalent quantity of income and saving as described earlier. I think you question this off the top while I have claimed it must be the case. But please suspend disbelief for purposes of what I want to describe next, because given that assumed starting point, this should at least reinforce the idea that S = I at all times following that same assumption for the investment injection.

It must be the case, if you define income and expenditure to be identical. If you define them so that they are not identical, which seems both possible and reasonable, then savings and investment are also not identical.

So now assume that the first round of the multiplier math works and there is an initial consumption burst of quantity 66, representing the MPC effect on the income of 100 that was just newly created.

And correspondingly there is new saving of 33.

A pertinent question then is how this gets reflected in income accounting.

As a simplification, assume that the factors of the investment good production who received the new income of 100 are the ones who spend the 66.

So the economy has earned 100 in its factors of investment good production capacity and has now spent 66 in its MPC capacity.

Recall that at the investment injection stage considered on its own, before the multiplier starts to work, the economy saved 100.

Yes, that’s fine if income does accrue simultaneously with expenditure, but that depends on how one chooses to define and measure income, and I don’t feel obligated to adopt the standard accounting definition under all circumstances. (And is it really the case that only one way of defining income is countenanced by accountants?) At any rate, in my first iteration of the lagged model, I specified the lag so that income was earned by households at the end of the period with consumption becoming a function of income in the preceding period. In that setup, the accounting identities were indeed satisfied. However, even with the lag specified that way, the main features of the adjustment process stressed in textbook treatments – frustrated plans, and involuntary inventory accumulation or decumulation – were absent.

Then, in the first stage of the multiplier, the economy spent 66 on consumption. For simplicity of exposition, I’ve assumed those who initially saved were the ones who then spent (I.e. the factors of investment production) But no more income has been assumed to be earned by them. So they have dissaved 66 in the second stage. At the same time, those who produced the 66 of consumer goods have earned 66 as factors of production for those consumer goods. But the consumer goods they produced have been purchased. So there are no remaining consumer goods for them to purchase with their income of 66. And that means they have saved 66.

Therefore, the net saving result of the first round of the multiplier effect is 0.

Thus an MPS of 1/3 has resulted in 0 incremental saving for the macroeconomy. That is because the opening saving of 100 by the factors of production for the investment good has only been redistributed as cumulative saving as between 33 for the investment good production factors and 66 for the consumer good production factors. So the amount of cumulative S still equals the amount of original S, which equals I. And the important observation is that the entire quantity of saving was created originally and at the outset as equivalent to the income earned by the factors of the investment good production.

There is no logical problem here given the definitional imputation of income to households in the initial period before any payments to households have actually been made. However, the model has to be reinterpreted so that household consumption and savings decisions are a function of income earned in the previous period.

Each successive round of the multiplier features a similar combination of equal dissaving and saving.

The result is that cumulative saving remains constant at 100 from the outset and I = S remains in tact always.

The important point is that an original investment injection associated with a Keynesian multiplier process accounts for all the macroeconomic saving to come out of that process, and the MPS fallout of the MPC sequence accounts for none of it.

That is fine, but to get that result, you have to amend the basic Keynesian model or make consumption a function the previous period’s income, which is consistent with what I showed in my first iteration of the lagged model. But that iteration also showed that savings has a somewhat different meaning from the meaning usually attached to the term, saving or dissaving corresponding to a passive accumulation of funds associated with income exceeding or falling short of what it was expected to be in a given period.

JKH followed up this comment with another one explaining how, within the basic Keynesian model, a change in investment (or in some other expenditure parameter) causes a sequence of adjustments from the old equilibrium to a new equilibrium.

Assume the economy is at an alleged equilibrium point – at the intersection of a planned expenditure line with the 45 degree line.

Suppose planned investment falls by 100. Again, assume MPC = 2/3.

The scenario is one in which investment will be 100 lower than its previous level (bearing in mind we are referring to the level of investment flows here).

Using comparable logic as in my previous comment, that means that both I and S drop by 100 at the outset. There is that much less investment injected and saving created as a result of the economy not operating at a counterfactual level of activity equal to its previous pace.

So expenditure drops by 100 – and that considered just on its own can be represented by a direct vertical drop from the previous equilibrium point down to the planning line.

But as I have said before, such a point is unrealizable in fact, because it lies off the 45 degree line. And that corresponds to the fact that I of 100 generates S of 100 (or in this case a decline in I from previous levels means a decline in S from previous levels). So what happens is that instead of landing on that 100 vertical drop down point, the economy combines (in measured effect) that move with a second move horizontally to the left, where it lands on the 45 degree line at a point where both E and Y have declined by 100. This simply reflects the fact that I = S at all times as described in my previous comment (which again I realize is a contentious supposition for purposes of the broader discussion).

Actually, it is clear that being off the 45-degree line is not a matter of possibility in any causal or behavioral sense, but is simply a matter of how income and expenditure are defined. With income and expenditure suitably defined, income need not equal expenditure. As just shown, if one wants to define income and expenditure so that they are equal at all times, a temporal adjustment process can be derived if current consumption is made a function of income in the previous period (presumably with an implicit behavioral assumption that households expect to earn the same income in the current period that they earned in the previous period). The adjustment can be easily portrayed in the familiar Keynesian cross, provided that the lag is incorporated into the diagram by measuring E(t) on the vertical axis and measures Y(t-1) on the horizontal axis. The 45-degree line then represents the equilibrium condition that E(t) = Y(t-1), which implies (given the implicit behavioral assumption) that actual income equals expected income or that income is unchanged period to period. Obviously, in this setup, the economy can be off the 45-degree line. Following a change in investment, an adjustment process moves from the old expenditure line to the new one continuing in stepwise fashion from the new expenditure line to the 45-degree line and back in successive periods converging on the point of intersection between the new expenditure line and the 45-degree line.

This happens in steps representable by discrete accounting. Common sense suggests that a “plan” can consist of a series of such discrete steps – in which case there is a ratcheting of reduced investment injections down the 45 degree line – or a plan can consist of a single discrete step depending on the scale or on the preference for stepwise analysis. The single discrete step is the clearest way to analyse the accounting record for the economics.

There is no such “plan” in the model, because no one foresees where the adjustment is leading; households assume in each period that their income will be what it was in the previous period, and firms produce exactly what consumers demand without change in inventories. However, all expenditure planned at the beginning of each period is executed (every household remaining on its planned expenditure curve), but households wind up earning less than expected in each period. Suitably amended, I consider this statement to be consistent with Lipsey’s critique of standard textbook expositions of the Keynesian cross adjustment process wherein the adjustment to a new equilibrium is driven by the frustration of plans.

Finally, some brief responses to JKH’s comments on handling lags.

I’m going to refer to standard accounting for Y as Y and the methodology used in the post as LGY (i.e. “Lipsey – Glasner income” ).

Then:

E ( t ) = Y ( t )

E ( t ) = LGY ( t +1)

Standard accounting recognizes income in the time period in which it is earned.

LGY accounting recognizes income in the time period in which it is paid in cash.

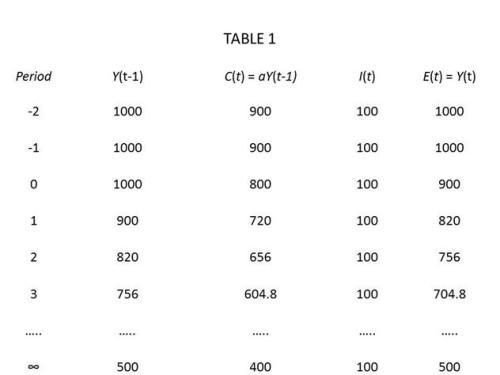
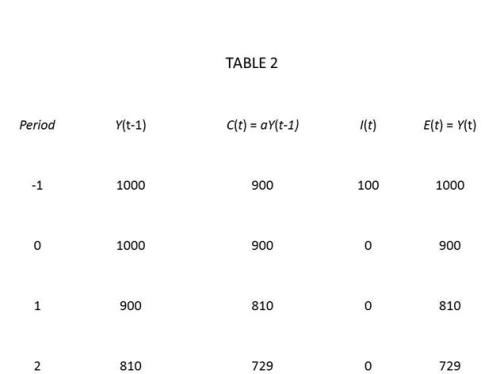
Consider the point in table 1 where the MPC propensity factor drops from .9 to .8. . . .

In the first iteration, E is 900 ( 100 I + 800 C ) but LGY is 1000.

Household saving is shown to be 200.

Here is how standard accounting handles that:

First, a real world example. Suppose a US corporation listed on a stock exchange reports its financial results at the end of each calendar quarter. And suppose it pays its employees once a month. But for each month’s work it pays them at the start of the next month.

Then there is no way that this corporation would report it’s December 31 financial results without showing a liability on its balance sheet for the employee compensation earned in December but not yet paid by December 31. . . .

In effect, the employees have loaned the corporation one months salary until that loan is repaid in the next accounting period.

The corporation will properly list a liability on its balance sheet for wages not yet paid. This may be a “loan in effect,” but employees don’t receive an IOU for the unpaid wages because the wages are not yet due. I am no tax expert, but I am guessing that a liability to pay taxes on the wages owed to, but not yet received by, employees is incurred until the wages are paid, notwithstanding whatever liability is recorded on the books of the corporation. A worker employed in 2014, but not paid until 2015, will owe taxes on his 2015, not 2014, tax return. A “loan in effect” is not the same as an actual payment.

This is precisely what is happening at the macro level in the LGY lag example.

So the standard national income accounting would show E = Y = 900, with a business liability of 900 at the end of the period. Households would have a corresponding financial asset of 900.

The “financial asset” in question is a fiction. There is a claim, but the claim at the end of the period has not fallen due, so it represents a claim to an expected future payment. I expect to get a royalty check next month, for copies of my book sold last year. I don’t consider that I have received income until the check arrives from my publisher, regardless of how the publisher chooses to record its liability to me on its books. And I will not pay any tax on books sold in 2014 until 2016 when I file my 2015 tax return. And I certainly did not consider the expected royalties as income last year when the books were sold. In fact, I don’t know — and never will — when in 2014 the books were sold.

Back at the beginning of that same period, business repaid the prior period liability of 1000 to households. But they received cash revenue of 900 during the period. So as the post says, business cash would have declined by 100 during the period.

This component of 100 when received by households is part of a loan repayment in effect. This does not constitute a component of standard income accounting Y or S for households. This sort of thing is captured In flow of funds accounting.

Just as LGY is the delayed payment of Y earned in the previous period, LGS overstates S by the difference between LGY and Y.

For example, when E is 900, LGY is 1000 and Y is 900. LGS is 200 while S is 100.

So under regular accounting, this systematic LG overstatement reflects the cash repayment of a loan – not the differential receipt of income and saving.

That is certainly a possible interpretation of the assumptions being made, but obviously there are alternative interpretations that are completely consistent with workings of the basic Keynesian model.

And another way of describing this is that households earn Y of 900 and get paid in the same period in the form of a non-cash financial asset of 900, which is in effect a loan to business for the amount of cash that business owes to households for the income the latter have already earned. That loan is repaid in the next period.

Again, I observe that “payments in effect” are being created to avoid working with and measuring actual payments as they take place. I have no problem with such “payments in effect,” but that does not mean that the the magnitudes of interest can be measured in only one way.

There are several ironies in the comparison of LG accounting with standard accounting.

First, using standard accounting in no way impedes the analysis of cash flow lags. In fact, this is the reason for separate balance sheet and flow of funds accounting – so as not to conflate cash flow analysis with the earning of income when there are clear separations between the earning of income and the cash payments to the recipients of that income. The 3 part framework is precise in its treatment of such situations.

Not sure where the irony is. In any event, I don’t see how the 3 part framework adds anything to our understanding of the Keynesian model.

Second, in the scenario constructed for the post, there is no logical connection between a delayed income payment of 1000 and a decision to ramp down consumption propensity. Why would one choose to consume less because an income payment is systematically late? If that was the case, one would ramp down consumption every time a payment was delayed. But every such payment is delayed in this model. Changes in consumption propensity cannot logically be a systematic function of a systematic lag – or consumption propensity would systematically approach 0, which is obviously nonsensical.

This seems to be a misunderstanding of what I wrote. I never suggested that the lag between expenditure and income is connected (logically or otherwise) to the reduction in the marginal propensity to consume. A lag is necessary for there to be a sequential rather than an instantaneous adjustment process to a parameter change in the model, such as a reduced marginal propensity to consume. There is no other connection.

Third, my earlier example of a corporation that delayed an income payment from December until January is a stretch on reality. Corporations have no valid reason to play such cash management games that span accounting periods. They must account for legitimate liabilities that are outstanding when proceeding to the next accounting period.

I never suggested that corporations are playing a game. Wage payments, royalty and dividend payments are made according to fixed schedules, which may not coincide with the relevant time period for measuring economic activity. Fiscal years and calendar years do not always coincide.

Shorter term intra period lags may still exist – as within a one month income payment cycle. But again, so what? There cannot be systemic behavior to reduce consumption propensity due to systematic lags. Moreover, a lot of people get paid every 2 weeks. But that is not even the relevant point. Standard accounting handles any of these issues even at the level of internal management accounting accruals between external financial reporting dates.

I never suggested that the propensity to consume is related to the lag structure in the model. The propensity to consume determines the equilibrium; the lag structure determines the sequence of adjustments, following a change in a spending parameter, from one equilibrium to another.

PS I apologize for this excessively long — even by my long-winded and verbose standards — post.

Why Theories of National Income Based on Accounting Identities Are Nonsensical and Error-Ridden, Part III

Published March 11, 2015 accounting identities , R. G. Lipsey , savings-investment identity 30 Comments

In my previous post, I argued that an accounting identity, which tells us that two expressions are defined to be the same, must hold in every state of the world, and therefore could not be disproved by any conceivable observation. So if I define savings and investment (or income and expenditure) to be the same thing, I am simply restricting my semantic description of the world, I am not restricting in any way the set of observable states of the world that conform to my semantic convention. An accounting identity therefore has no empirical content, which means that the accounting identity between savings and investment cannot explain the process by which a macroeconomic model adjusts to a parametric change in the model, traversing from a pre-existing equilibrium with savings and investment being equal to a new equilibrium with savings and investment equal.

In his paper, “The Foundations of the Theory of National Income,” which I am attempting to summarize and explain in this series of posts, R. G. Lipsey provides a numerical example of such an adjustment path. And it will be instructive to follow that path in some detail. The key point about this model is the assumption that households decide how much to save and consume in the current period based on the disposable income received in the previous period. The assumption that all receipts of the business firms are paid out to owners and providers of factor services at the end of each period is a behavioral assumption (not an accounting identity) that rules out any change in the retained earnings held by firms. If firms were accumulating financial assets, then their payments to households would not match their receipts. The following simple model reflects a one-period lag (known as a Robertsonian lag) between household earnings and household consumption.

C(t) = aY(t-1) (behavioral assumption)

I(t) = I* (behavioral assumption)

E(t) ≡ C(t) + I(t) (accounting identity)

Y(t) ≡ C(t) + S(t) (accounting identity)

Y(t) = E(t) (behavioral assumption)

Y(t-1) = Y(t) (equilibrium condition)

Assume that the economy starts off with a = .9 and I(t) = 100. The system is easily solved for E = Y = 1000, with C = 900 and I = 100. Savings, which is the difference between Y and C, is 100, just equal to I. The definition of saving will have to be fleshed out further below. Now assume that there is a parametric change in a (the marginal propensity to consume) to .8 from .9. This change causes equilibrium income to fall from 1000 to 500. By assumption, investment is constant, so that in the new equilibrium saving remains equal to 100. The change in income is reflected in a drop in consumption from 900 to 400. But given the one-period lag between earnings and expenditure, we can follow how the system changes over time, moving closer and closer to the new equilibrium in each successive period, as shown in the following table.

Consider the following questions.

First, in the course of this period-by-period adjustment, will there be any unplanned investment?

Second, in this example, the parametric change — an increase in the propensity of households to save — may be described as an increase in planned savings by households. Planned investment is unchanged. With planned savings greater than planned investment, will the household plans to increase savings be frustrated (implying positive or negative unplanned savings) as alleged in proposition 3 in the list of erroneous propositions provided earlier in the first installment in this series (see appendix below).

The answer to the first question is: not necessarily. There is nothing to prevent us from assuming that all firms correctly anticipate the reduction in consumer demand, so that production falls along with consumption with no change in inventories. It is not necessary to assume that firms can foresee the future; it could be that all consumption is in the form of services, or that production is undertaken only in response to consumer orders. With inventories unchanged, there is no unplanned investment.

The answer to the second question is that it depends on what is meant by unplanned savings. Unplanned savings could mean that households wind up saving an amount other than the amount that they had intended to save at the beginning of the period; households intended to save 200 at the beginning of period 0, but because their income turned out to be only 900, instead of 1000, in period 0, household savings, under the accounting identity, is only 100 instead of 200. However, households intended to consume 800 in period 0, and that is the amount that they actually consumed. The only sense in which households did not execute their intended plans is that household income in period 0 was less than households had expected. Lipsey calls this a distinction between plans in the point sense, and plans in the schedule sense. In this scenario, while plans in the schedule sense are carried out, plans in the point sense are not, because households do not end up at the point on their consumption functions that they had expected to be on.

So the equilibrium condition above that income does not change from one period to the next can be restated as follows: the system is in equilibrium when planned savings equals realized savings. Planned savings is the unconsumed portion of households’ expected income, which is the income households earned in the previous period. The definition embodies a specific behavioral hypothesis about how households formulate their expectations of income in the future.

S_p_(t) ≡ Y(t-1) – C(t).

Realized savings is the unconsumed portion of households’ actual income in the current period. It can be written as

S_r_(t) ≡ Y(t) – C(t).

Or restated differently yet again, the equilibrium condition is that actual disposable income in period t equals expected disposable income in period t.

Let’s flesh out the behavioral assumptions behind this model in a bit more detail. Business firms disburse income to households (owners and providers of factor services) at the end of each period. Households decide how much to save and consume in the upcoming period after receiving their incomes from firms at the close of the previous period. Savings are in the form of bond purchases made at the start of the period. Based on the consumption and savings plans formulated by households at the start of the new period, firms decide how much output to produce and how much labor to hire to produce that output, firms immediately notifying households how many hours they will work in the upcoming period. However, households are committed to the consumption plans already made at the beginning of the period, so they must execute those plans even if the incomes earned during the period are less than anticipated.

In our example, by choosing to increase their savings to 200 through bond purchases at the beginning of the upcoming period, while reducing consumption from 900 to 800, households cause business firms to reduce output from 1000 to 900 (investment being unchanged), and to reduce employment (measured in terms of total hours worked) by 11.1%. After buying bonds equal to 200, households have 800 left in cash, with which they finance their purchases for the rest of the month. So it is not obvious that households were unable to execute any of their plans  during the period. However, at the end of the period, households receive only 900 in income from business firms, so although households did buy bonds equal to 200 at the start of the period, they carry over only 900 in cash into the next period, not 1000 as expected. Thus, realized savings are only 100 instead of 200, because household cash holding at the endo f the period turned out to be 100 less than expected. Nevertheless, it is difficult to identify any plan to save that was frustrated, inasmuch as households did purchase bonds equal to 200 at the beginning of the period, and did reduce consumption as planned. As Lipsey puts it:

[W]hether or not the actual real plans laid by households are frustrated depends on what plans households lay, i.e., it depends on our behaviour assumption, not on our definitions. If we assume that households make point plans about their bonds, and schedules plans about their transactions and precautionary balances, then no frustration of plans occurs.

If the statement quoted in (3) [see appendix below] is meant to have empirical content, it depends on a very specific hypothesis about households’ savings plans. These plans must be made in the point and not in the schedule sense, and the plans must include not only additions to the stock of income-earning assets, but also point-plans concerning transactions balances even though the household does not now know what level of transactions the balances will be required to facilitate. . . .

[W]e are now in a position to see what is wrong with statement (2), that actual savings must always equal actual investment, and statement (5), which draws the analogy with demand and supply analysis. Consider statement (2) first.

In the General Theory, Keynes stressed the fact that savings and investment decisions are made by different groups and that there is thus, no reason why planned investment should equal planned savings. [It has been argued] that, although plans can differ, actual realised saving must always be equal to actual realised investment, and, therefore, when planned savings does not equal planned investment, either the plans of savers, or of investors, must be frustrated. Of course, it is quite possible to define savings and investment so that they are the same thing, but it is a basic error to equate the magnitude so defined with the magnitude about which savers actually lay plans. Since ex post S and I as defined bear no relation to the magnitudes about which savers actually make plans, we can deduce nothing about what happens when ex ante S is not equal to ex ante I from the fact that we chose to use the terms ex post S and ex post I to refer to a single, and different, magnitude. The basic error arises from the assumption that households and firms make plans about the same magnitude when they are planning their savings and investment. The traditional theory defines investment as goods produced and not sold to households (= capital goods plus changes in inventories). According to our theory of the behaviour of firms, this is what firms do lay plans about: they plan to add so many capital goods and so many inventories to their existing holdings. The theory then says I ≡ S, and , thus, builds in the implicit assumption that households lay plans about the same magnitude. But according to the standard theory of household behaviour, they do not do so! Households, not subject to money illusion, are assumed to wish to lay aside a certain quantity of real purchasing power which is either used to increase the holdings of cash or used to purchase bonds. There is nothing in the standard theory of household behaviour that leads us to hypothesise that households care whether or not there exists – produced but unconsumed – a physical stock of goods which is the counterpart of the money they have laid aside. Indeed why should they? All they are assumed to care about is the potential real purchasing power of their savings, and this depends only on the amount of money saved, the present price level, and the expected future price level.

This is one of the keys to the whole present confusion: households lay plans about a magnitude that is different from the one that firms lay plans about. Firms plan to have produced and unconsumed a certain quantity of goods, while households plan to leave unspent a certain quantity of purchasing power. This means that it is quite possible for planned investment to differ from planned savings and to have both sets of plans fulfilled so that actual, realized investment differs from actual realized savings. [footnote: Now, of course, we mean by realised S and I the realised magnitudes about which firms and households are actually laying plans. This, of course, does not interfere with the statistician saying that realised savings is identical with realised investment since he refers to a different magnitude when he speaks of realised savings.]

Now consider another variation of the numerical example in Table 1. Instead of a change in the propensity to consume in period 0, assume instead that planned investment drops from 100 to 0. Starting with period -1, Table 2 displays the same initial equilibrium as in Table 1. Because we make a behavioral hypothesis that inventories do not change, planned and realized investment must be zero in period 0 and in all subsequent periods.

According to the national-income identities, savings must equal zero because investment is zero. But what is the actual behavior that corresponds to zero saving? In period 0, households carried over 1000 in cash from period -1. From that 1000, they used 100 to buy bonds and spent the remainder of their disposable incomes on consumption goods. So households planned to save 100 and consume 900, and it appears that they succeeded in executing their plans. But according to the national-income identities, they failed to execute their plan to save 100, and saved only 0, presumably because there were unintended savings of -100 that cancelled out the planned (and executed) savings of 100. So it appears that we have come up against something of a paradox. Here is Lipsey’s solution of the paradox.

[A]ny definitions are possible if consistently used, but this use of the word “unintended” has nothing to do with intended and unintended behaviour. To preserve the identity we must say that the plans of households were frustrated because a real counterpart of the saving they successfully made was not produced. We may say this if we wish, but the danger is that we will think we have said something about the world, and about the actual experiences of households. Indeed, a perusal of established textbooks shows that this confusion has occurred over and over again.

Thus, we conclude that, when we define investment as production not consumed, and savings as income [not consumed] . . . there is no reason why actual savings should not differ from actual investment.

Finally, what about the analogy between savings and investment in macro analysis and demand and supply in micro analysis as in erroneous statement (4) (see appendix)? If we write demand for some good as a function of the price of the good

D = D(p),

and write the supply of some good as a function of the price of the good

S = S(p),

then our equilibrium condition is simply D = S, where D represents desired purchases of the good, and S represents desired sales of the good. Because the act of selling logically entails the activity of purchasing, a purchase and a sale are merely different names for the same thing. So the plans of demanders to buy and the plans of suppliers to sell are plans about the same thing. The plans of demanders to buy and the plans of suppliers to sell cannot be fulfilled simultaneously unless there is an equilibrium in which demand equals supply. The difference between the microeconomic equilibrium in which demand equals supply and the macroeconomic equilibrium in which savings equals investment is that suppliers and demanders in a market are making plans about the same magnitude: sales (aka purchases) of a good. However,

in the national income case the two sets of real plans (savers’ and investors’) are laid about two different magnitudes. Thus the analogy often draw between the two theories in respect of plans and realized quantities is an incorrect one.

Appendix: List of Erroneous Propositions

1 The equilibrium of the basic Keynesian model is given by the intersection of the aggregate demand (i.e., expenditure) function and the 45-degree line representing the accounting identity E ≡ Y.

2 Although people may try to save different amounts from what people try to invest, savings can’t be different from investment; realized (ex post) savings necessarily always equals realized (ex post) investment.

3 Out of equilibrium, planned savings do not equal planned investment, so it follows from (2) that someone’s plans are being disappointed, and there must be either unplanned savings or dissavings, or unplanned investment or disinvestment

4 The simultaneous fulfilment of the plans of savers and investors occurs only when income is at its equilibrium level just as the plans of buyers and sellers can be simultaneously fulfilled only at the equilibrium price.

5 Whenever savers (households) plan to save an amount different from what investors (business firms) plan to invest, a mechanism operates to ensure that realized savings remain equal to realized investment, despite the attempts of savers and investors to make it otherwise. Indeed, this mechanism is what causes dynamic change in the circular flow of income and expenditure.

6 Since the real world, unlike the simple textbook model, contains a very complex set of interactions, it is not easy to see how savings stay equal to investment even in the worst disequilibrium and the most rapid change.

7 The dynamic behavior of the Keynesian circular flow model in which disequilibrium implies unintended investment or disinvestment can be shown by moving upwards or downwards along the gap between the expenditure function and the 45-degree line in the basic Keynesian model.

CAUTION Accounting Identity Handle with Care

Published February 11, 2015 accounting identities , Hawtrey , Keynes , R. G. Lipsey , Scott Sumner 17 Comments
Tags: ,

About three years ago, early in my blogging career, I wrote a series of blog posts (most or all aimed at Scott Sumner) criticizing him for an argument in a blog post about the inefficacy of fiscal stimulus that relied on the definitional equality of savings and investment. Here’s the statement I found objectionable.

Wren-Lewis seems to be . . . making a simple logical error (which is common among Keynesians.)  He equates “spending” with “consumption.”  But the part of income not “spent” is saved, which means it’s spent on investment projects.  Remember that S=I, indeed saving is defined as the resources put into investment projects.  So the tax on consumers will reduce their ability to save and invest.

I’m not going to quote any further from that discussion. If you’re interested here are links to the posts that I wrote (here, here, here, here, here, and this one in which I made an argument so obviously false that, in my embarrassment, I felt like giving up blogging, and this one in which I managed to undo, at least partially, the damage of the self-inflicted wound). But, probably out of exhaustion, that discussion came to an inconclusive end, and Scott and I went on with our lives with no hard feelings.

Well, in a recent post, Scott has again invoked the savings-equals-investment identity, so I am going to have to lodge another protest, even though I thought that, aside from his unfortunate reference to the savings-investment identity, his post made a lot of sense. So I am going to raise the issue one more time – we have had three years to get over our last discussion – hoping that I can now convince Scott to stop using accounting identities to make causal statements.

Scott begins by discussing the simplest version of the income-expenditure model (aka the Keynesian cross or 45-degree model), while treating it, as did Keynes, as if it were interchangeable with the national-accounting identities:

In the standard national income accounting, gross domestic income equals gross domestic output.  In the simplest model of all (with no government or trade) you have the following identity:

NGDI = C + S = C + I = NGDP  (it also applies to RGDI and RGDP)

Because these two variables are identical, any model that explains one will, ipso facto, explain the other.

There is a lot of ground to cover in these few lines. First of all, there are actually three relevant variables — income, output, and expenditure – not just two. Second aggregate income is not really the same thing as consumption and savings. Aggregate income is constituted by the aggregate earnings of all factors of production. However, an accounting identity assures us that all factor incomes accruing to factors of production, which are all ultimately owned by the households providing services to business firms, must be disposed of either by being spent on consumption or by being saved. Aggregate expenditure is different from aggregate income; expenditure is constituted not by the earnings of households, but by their spending on consumption and by the spending of businesses on investment, the purchase of durable equipment not physically embodied in output sold to households or other businesses. Aggregate expenditure is very close to but not identical with aggregate output. They can differ, because not all output is sold, some of it being retained within the firm as work in progress or as inventory. However, in an equilibrium situation in which variables were unchanging, aggregate income, expenditure and output would all be equal.

The equality of these three variables can be thought of as a condition of macroeconomic equilibrium. When a macroeconomic system is not in equilibrium, aggregate factor incomes are not equal to aggregate expenditure or to aggregate output. The inequality between factor incomes and expenditure induces further adjustments in spending and earnings ultimately leading to an equilibrium in which equality between those variables is restored.

So what Scott should have said is that because NGDI and NGDP are equal in equilibrium, any model that explains one will, ipso facto, explain the other, because the equality between the two is the condition for finding a solution to the model. It therefore follows that savings and investment are absolutely not the same thing. Savings is the portion of household earnings from providing factor services that is not spent on consumption. Investment is what business firms spend on plant and equipment. The two magnitudes are obviously not the same, and they do not have to be equal. However, equality between savings and investment is, like the equality between income and expenditure, a condition for macroeconomic equilibrium. In an economy not in equilibrium, savings does not equal investment. But the inequality between savings and investment induces adjustments that, in a stable macroeconomic system, move the economy toward equilibrium. Back to Scott:

Nonetheless, I think if we focus on NGDI we are more likely to be able to think clearly about macro issues.  Consider the recent comment left by Doug:

Regarding Investment, changes in private investment are the single biggest dynamic in the business cycle. While I may be 1/4 the size of C in terms of the contribution to spending, it is 6x more volatile. The economy doesn’t slip into recession because of a fluctuation in Consumption. Changes in Investment drive AD.

This is probably how most people look at things, but in my view it’s highly misleading. Monetary policy drives AD, and AD drives investment. This is easier to explain if we think in terms of NGDI, not NGDP.  Tight money reduces NGDI.  That means the sum of nominal consumption and nominal saving must fall, by the amount that NGDI declines.  What about real income?  If wages are sticky, then as NGDI declines, hours worked will fall, and real income will decline.

So far we have no reason to assume that C or S will fall at a different rate than NGDI. But if real income falls for temporary reasons (the business cycle), then the public will typically smooth consumption.  Thus if NGDP falls by 4%, consumption might fall by 2% while saving might fall by something like 10%.  This is a prediction of the permanent income hypothesis.  And of course if saving falls much more sharply than gross income, investment will also decline sharply, because savings is exactly equal to investment.

First, I observe that consumption smoothing and the permanent-income hypothesis are irrelevant to the discussion, because Scott does not explain where any of his hypothetical numbers come from or how they are related. Based on commenter Doug’s suggestion that savings is ¼ the size of consumption, one could surmise that a 4% reduction in NGDP and a 2% reduction in consumption imply a marginal propensity to consumer of 0.4. Suppose that consumption did not change at all (consumption smoothing to the max), then savings, bearing the entire burden of adjustment, would fall through the floor. What would that imply for the new equilibrium of NGDI? In the standard Keynesian model, a zero marginal propensity to consume would imply a smaller effect on NGDP from a given shock than you get with an MPC of 0.4.

It seems to me that Scott is simply positing numbers and performing calculations independently of any model, and then tells us that the numbers have to to be what he says they are because of an accounting identity. That does not seem like an assertion not an argument, or, maybe like reasoning from a price change. Scott is trying to make an inference about how the world operates from an accounting identity between two magnitudes. The problem is that the two magnitudes are variables in an economic model, and their values are determined by the interaction of all the variables in the model. Just because you can solve the model mathematically by using the equality of two variables as an equilibrium condition does not entitle you to posit a change in one and then conclude that the other must change by the same amount. You have to show how the numbers you have posited are derived from the model.

If two variables are really identical, rather than just being equal in equilibrium, then they are literally the same thing, and you can’t draw any inference about the real world from the fact that they are equal, there being no possible state of the world in which they are not equal. It is only because savings and investment are not the same thing, and because in some states of the world they are not equal, that we can make any empirical statement about what the world is like when savings and investment are equal. Back to Scott:

This is where Keynesian economics has caused endless confusion.  Keynesians don’t deny that (ex post) less saving leads to less investment, but they think this claim is misleading, because (they claim) an attempt by the public to save less will boost NGDP, and this will lead to more investment (and more realized saving.)  In their model when the public attempts to save less (ex ante), it may well end up saving more (ex post.)

I agree that Keynesian economics has caused a lot of confusion about savings and investment, largely because Keynes, who, as a philosopher and a mathematician, should have known better, tied himself into knots by insisting that savings and investment are identical, while at the same time saying that their equality was brought about, not by variations in the rate of interest, but by variations in income. Hawtrey, Robertson, and Haberler, among others, pointed out the confusion, but Keynes never seemed to grasp the point. Textbook treatments of national-income accounting and the simple Keynesian cross still don’t seem to have figured this out. But despite his disdain for Keynesian economics, Scott still has to figure it out, too. The best place to start is Richard Lipsey’s classic article “The Foundations of the Theory of National Income: An Analysis of Some Fundamental Errors” (a gated link is available here).

Scott begins by sayings that Keynesians don’t deny that (ex post) less saving leads to less investment. I don’t understand that assertion at all; Keynesians believe that a desired increase in savings, if desired savings exceeded investment, leads to a decrease in income that reduces saving. But the abortive attempt to increase savings has no effect on investment unless you posit an investment function (AKA an accelerator) that includes income as an independent variable. The accelerator was later added to the basic Keynesian model Hicks and others in order to generate cyclical fluctuations in income and employment, but non-Keynesians like Ralph Hawtrey had discussed the accelerator model long before Keynes wrote the General Theory. Scott then contradicts himself in the next sentence by saying that Keynesians believe that by attempting to save less, the public may wind up saving more. Again this result relies on the assumption of an accelerator-type investment function, which is a non-Keynesian assumption. In the basic Keynesian model investment is determined by entrepreneurial expectations. An increase (decrease) in thrift will be self-defeating, because in the new equilibrium income will have fallen (risen) sufficiently to reduce (increase) savings back to the fixed amount of investment entrepreneurs planned to undertake, entrepreneurial expectations being held fixed over the relevant time period.

I more or less agree with the rest of Scott’s post, but Scott seems to have the same knee-jerk negative reaction to Keynes and Keynesians that I have to Friedman and Friedmanians. Maybe it’s time for both of us to lighten up a bit. Anyway in honor of Scott’s recent appoint to the Ralph Hawtrey Chair of Monetary Policy at the Mercatus Center at George Mason University, I will just close with this quotation from Ralph Hawtrey’s review of the General Theory (chapter 7 of Hawtrey’s Capital and Employment) about Keynes’s treatment of savings and investment as identically equal.

[A]n essential step in [Keynes’s] train of reasoning is the proposition that investment and saving are necessarily equal. That proposition Mr. Keynes never really establishes; he evades the necessity doing so by defining investment and saving as different names for the same thing. He so defines income to be the same thing as output, and therefore, if investment is the excess of output over consumption, and saving is the excess of income over consumption, the two are identical. Identity so established cannot prove anything. The idea that a tendency for investment and saving to become different has to be counteracted by an expansion or contraction of the total of incomes is an absurdity; such a tendency cannot strain the economic system, it can only strain Mr. Keynes’s vocabulary.

About Me

David Glasner
Washington, DC

I am an economist in the Washington DC area. My research and writing has been mostly on monetary economics and policy and the history of economics. In my book Free Banking and Monetary Reform, I argued for a non-Monetarist non-Keynesian approach to monetary policy, based on a theory of a competitive supply of money. Over the years, I have become increasingly impressed by the similarities between my approach and that of R. G. Hawtrey and hope to bring Hawtrey’s unduly neglected contributions to the attention of a wider audience.

My new book Studies in the History of Monetary Theory: Controversies and Clarifications has been published by Palgrave Macmillan

Follow me on Twitter @david_glasner

Archives

Enter your email address to follow this blog and receive notifications of new posts by email.

Join 3,272 other subscribers
Follow Uneasy Money on WordPress.com